Torsi

Torsi sama dengan gaya pada gerak translasi. Torsi menunjukkan kemampuan sebuah gaya untuk membuat benda melakukan gerak rotasi. Sebuah benda akan berotasi bila dikenai torsi. Perhatikan pada sebuah pintu, coba bandingkan apabila kita mendorong pintu pada ujung pintu dengan kita mendorong pada bagian tengah pintu. Mana yang lebih mudah untuk membuka pintu? Kita akan merasakan gaya yang diperlukan untuk mendorong pintu agar terbuka akan lebih ringan apabila dibandingkan dengan mendorong di ujung pintu.

Torsi

Jika pada sebuah benda diberikan gaya sebesar F maka benda akan memiliki percepatan yang disebabkan oleh gaya tersebut. Percepatan benda memiliki arah yang sama dengan arah gaya yang diberikan padanya. Bagaimana dengan benda yang berotasi? Bagaimana gayanya?

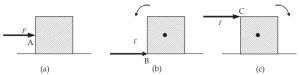
1. sebuah balok diberi gaya F, benda akan bertranslasi, jika balok di bagian tengah dipaku sehingga balok tidak dapat bertanslasi tapi dapat berotasi,
2. bila gaya diberikan pada sudut B benda akan berotasi, dengan arah berbeda dengan (b),
3. begitu juga bila diberikan pada sudut C

Besarnya torsi tergantung pada gaya yang dikeluarkan serta jarak antara sumbu putaran dan letak gaya. Mari kita tinjau sebuah batang dengan salah satu ujungnya berupa engsel tetapi masih bisa bergerak memutar. Misalnya ujung yang dipatri adalah ujung yang kita letakan di titik (0,0,0) dan ujung satunya merupakan ujung yang bebas adalah ujung satunya. Batang kita letakan pada sumbu x.

Pada benda dengan salah satu ujungnya berupa engsel sehingga tidak dapat bertranslasi tapi bisa berotasi. Diberi gaya dengan berbagai arah. Ditunjukkan juga skema gaya dan posisinya sebagai berikut.

1. arah r sejajar dengan arah F,
2. arah r tegak lurus dengan arah F,
3. arah r membentuk sudut θ terhadap F.

Jika gaya yang kita berikan sejajar dengan arah batang ternyata batang tidak berotasi. Kita dapat melihat skema pada pada gambar a diatas. Jika arah gaya tegak lurus maka batang akan berotasi. Seperti yang ditunjukkan gambar b diatas.

Bagaimana kalau gaya membentuk sudut θ yang besarnya sembarang dengan batang? Jika gaya membentuk sudut sembarang terhadap batang, benda akan berotasi tetapi percepatan sudut yang dihasilkan akan berbeda dengan jika sudutnya tegak lurus. Hal itu ditunjukkan pada gambar c diatas. Perhatikanlah arah putaran akan barlawanan bila gaya yang diberikan berlawanan arah.

Torsi disebut juga momen gaya dan merupakan besaran vektor. Torsi adalah hasil per silang antara vektor posisi r dengan gaya F, dapat dituliskan

besarnya torsi adalah :

Pada batang di atas vektor r adalah vektor yang berawal di ujung batang yang dipatri dan berujung atau berarah di ujung yang lainnya. Bila gaya tegak lurus maka θ = 90 sehingga nilai sin θ = 1. Torsi yang dilakukan pada batang maksimal. Bila 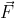 sejajar dengan 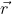, maka nilai sin θ = 0 sehingga besarnya torsi 0 dan batang tidak berotasi. Besar torsi dapat kita tuliskan sebagai :

dengan l =r sin θ

Arah Torsi

Lengan torsi ditunjukkan oleh l. Lengan torsi sebuah gaya didefinisikan sebagai panjang garis yang ditarik di titik sumbu rotasi sampai memotong tegak lurus garis kerja gaya seperti pada gambar berikut.

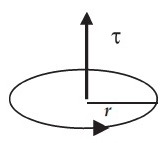
Perhatikan dengan arah torsi, arah torsi menuruti aturan putaran tangan kanan seperti pada gambar berikut.

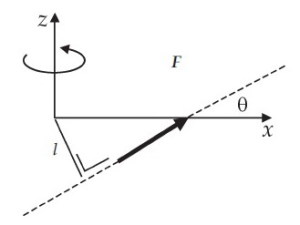
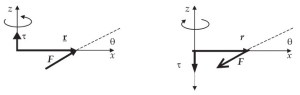
Jika arah putaran berlawanan dengan arah jarum jam maka arah torsi ke atas, dan arah bila arah putaran searah dengan arah putaran jarum jam maka arah torsi ke bawah. Kita dapat melihatnya dengan sebuah sistem koordinat. Bila batang terletak pada sumbu x dan pangkal vektor r di titik (0,0,0). Gaya pada arah sumbu y positif batang akan berputar melawan arah jarum jam, arah torsi ke arah sumbu z positif. Sebaliknya bila arah gaya kearah sumbu y negatif, putaran batang berlawanan dengan arah jarum jam, arah torsi ke sumbu z negatif. Jika arah gaya tidak tepat pada arah sumbu y tetapi membentuk sudut θ terhadap sumbu x, maka arah torsi dapat dilihat pada gambar berikut.

Arah torsi untuk F berarah sembarang. Arah sumbu y positif adalah arah masuk bidang gambar.

1. torsi memiliki arah ke sumbu z positif, tetapi arah putarannya berlawanan arah dengan arah jarum jam,
2. arah torsi ke sumbu z negatif, arah putarannya searah dengan arah jarum jam.

Jika pada sebuah benda bekerja lebih dari satu torsi bagaimana dengan gerakan benda? Jika pada benda bekerja lebih dari 1 torsi maka torsi total adalah jumlahan dari seluruh torsi yang bekerja.

Pada batang dengan titik tumpu pada ujung kiri batang, ada dua gaya yang bekerja pada batang.

Pada gambar diatas gaya F₁ akan menyebabkan batang berputar searah dengan jarum jam, gaya F₂ akan menyebabkan benda berputar berlawanan arah dengan arah jarum jam. Torsi totaladalah jumlah kedua torsi tersebut.