Minggu, 01 Maret 2015

Titik Berat

Titik berat adalah titik tangkap gaya berat. Resultan dari seluruh gaya berat benda yang terdiri atas bagian-bagian kecil benda dinamakan gaya berat. Sebuah benda terdiri atas banyak partikel. Setiap partikel mempunyai massa. oleh karena itu, tiap partikel mempunyai berat dantitik berat yang berbeda-beda. Partikel-partikel tersebut masingmasing mempunyai gaya beratw1, w2, w3, …, wn dengan resultan gaya berat w.
Titik Berat

Menetukan Titik Berat

Dari definisi di atas maka letak titik berat dapat ditentukan dengan langkah-langkah sebagai berikut.

a. Bangun dan bidang simetris homogen

Untuk bangun atau bidang simetris dan homogen titik beratnya berada pada titik perpotongan sumbu simetrinya. Contohnya : bujur sangkar, balok kubus dan bola.
Titik Berat Bujur SangkarBujur sangkar

b. Bangun atau bidang lancip

Untung benda ini titik beratnya dapat ditentukan dengan digantung benang beberapa kali, titik potong garis-garis benang (garis berat) itulah yang merupakan titik beratnya. Dari hasil tersebut ternyata dapat diketahui kesamaannya seperti berikut.
Titik Berat KerucutBenda lancip
Untuk bidang lancip y0 = \frac{1}{3} h
Untuk bangun lancip y0 = \frac{1}{4} h

Bagian bola dan lingkaran

Untuk bagian bola yaitu setengah bola pejal dan bagian lingkaran yaitu setengah lingkaran.
Titik Berat Setengah BolaTitik berat bagian bola

d. Gabungan benda

Untuk gabungan benda-benda homogen, letak titik beratnya dapat ditentukan dari rata-rata jaraknya terhadap acuan yang ditanyakan. Rata-rata tersebut ditentukan dari momen gaya dan gaya berat.
X_{0}=\frac{\sum xw}{\sum w}
Y_{0}=\frac{\sum yw}{\sum w}
Perhatikan nilai w pada persamaan diatas. Nilai w tersebut dapat diubah-ubah sesuai besaran yang diketahui diantaranya seperti berikut.
  1. w = mg, g sama berarti w dapat diganti dengan massa benda. Dari alasan inilah titik berat disebut juga titik pusat massa.
    X_{0}=\frac{\sum yM}{\sum M}        dan        Y_{0}=\frac{\sum ym}{\sum m}
  2. Untuk benda homogen berarti massa jenis sama (ρ sama) dan m = ρ v berarti massa dapat diganti dengan volumenya.
    x_{0}=\frac{\sum xV}{\sum V}\textup{ dan }y_{0}=\frac{\sum yV}{\sum V}

Contoh Titik Berat Pada Benda

Untuk membuktikan dapat kita lakukan dengan meletakkan pensil atau penggaris di atas jari-jari seperti pada gambar di bawah? Dimanakah letaknya agar bisa seimbang? Tentu kita bisa memperkirakan bahwa tempatnya ada di tengah-tengahnya. Titik tepat di atas jari-jari kalian itulah yang merupakan titik berat batang pensil atau penggaris.
Contoh Titik Berat BendaContoh Titik Berat Benda
-

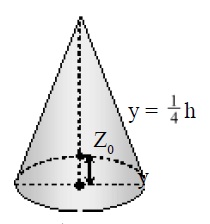
Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)

Entri yang Diunggulkan

Barru WanuAku