Kesetimbangan Partikel Dan Gerak Translasi

Syarat kesetimbangan partikel adalah jika partikel terletak pada bidang XY dan gaya-gaya yang bekerja diuraikan dalam komponen sumbu X dan sumbu Y. Partikel merupakan ukuran benda terkecil, sehingga sering digambarkan sebagai titik. Akibatnya, jika ada gaya yang bekerja pada partikel, maka gaya tepat mengenai pada pusat massa benda. Oleh karena itu, partikel hanya mengalami gerak translasi (menggeser). Gerak translasi merupakan gerak yang memenuhi hukum II Newton. Sehingga syarat kesetimbangan partikel dapat ditulis ΣF_x = 0  danΣF_y = 0.

Banyak persoalan yang berhubungan dengan keseimbangan partikel akibat pengaruh tiga buah gaya. Untuk menyelesaikannya, Anda dapat menggunakan syarat keseimbangan. Secara sederhana Anda juga dapat menggunakan aturan sinus dalam segitiga.

Jika partikel pada diatas dalam keadaan seimbang, maka berlaku persamaan F₁ + F₂ + F₃ = 0.Berdasarkan aturan sinus dalam segitiga, diperoleh persamaan .

Kesetimbangan Partikel

Penyebab gerak sumbu benda adalah gaya, dimana semakin besar gaya, maka semakin besar pula percepatan yang dialami. Partikel adalah benda yang ukurannya dapat diabaikan sehingga dapat digambarkan sebagai suatu titik materi. Akibatnya, jika gaya bekerja pada partikel titik tangkap gaya berada tepat pada partikel-partikel tersebut. Oleh karena itu, partikel hanya mengalami gerak translasi dan tidak mengalami gerak rotasi.

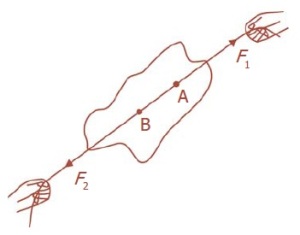
Resultan gaya sama dengan nol jika gaya sama besar, berlawanan arah dan garis kerjanya sama

Suatu partikel dikatakan dalam keadaan setimbang apabila resultan gaya yang bekerja pada partikel sama dengan nol.

ΣF = 0

Apabila partikel pada bidang xy, maka syarat kesetimbangan adalah resultan gaya pada komponen sumbu x dan sumbu y sama dengan nol.

ΣF_x = 0

ΣF_y = 0

Berdasarkan Hukum I Newton, jika resultan gaya yang bekerja pada benda sama dengan nol, maka percepatan benda menjadi nol. Artinya, bahwa partikel dalam keadaan diam atau bergerak dengan kecepatan tetap. Apabila partikel dalam keadaan diam disebut mengalami kesetimbangan statis, sedangkan jika bergerak dengan kecepatan tetap disebut kesetimbangan dinamis.

Resultan gaya sama dengan nol sehingga benda diam

Kesetimbangan Benda Tegar

Benda tegar adalah benda yang apabila dipengaruhi gaya-gaya tidak mengalami perubahan bentuk. Meskipun benda berotasi namun bentuknya tetap sehingga jarak antara partikel-partikelnya tetap.

Momen Kopel

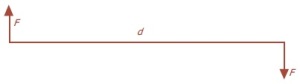
Kopel adalah pasangan dua buah gaya yang sejajar, sama besar, dan arahnya berlawanan. Pengaruh kopel terhadap sebuah benda adalah memungkinkan benda berotasi. Besarnya kopel dinyatakan dengan momen kopel yang merupakan hasil kali antara gaya dengan jarak antara kedua gaya tersebut.

Secara matematis dituliskan :

M = F.d

dengan:

M= momen kopel (Nm)
F = gaya (N)
d = jarak antara gaya (m)

Momen kopel merupakan besaran vektor. Momen kopel bertanda positif jika arah putarannya searah dengan putaran jarum jam dan negatif jika berlawanan dengan arah putaran jarum jam.

Momen gaya positif dan negatif

Menentukan Titik Tangkap Gaya Resultan

Pada bidang datar xy terdapat beberapa gaya F₁, F₂, dan F₃ saling sejajar dan bertitik tangkap di (x₁,y₁), (x₂,y₂), (x₃,y₃).

Sejumlah Gaya Bekerja pada Bidang XY

Resultan ketiga gaya tersebut adalah R yang bertitik tangkap di (x,y). Jika komponen gaya yang searah sumbu x adalah F_1x, F_2x, dan F_3x, sedangkan komponen gaya pada arah sumbu y adalah F_1y, F_2y, dan F_3y dengan jarak x₁, x₂, dan x₃ terhadap sumbu y, maka berlaku :

Στ _y = τ _1y + τ _2y + τ _3y

R_yx_R= F_1y.x₁ + F_2y.x₂ + F_3y.x₃

Dengan cara yang sama diperoleh :

Syarat Kesetimbangan Benda

Pada umumnya benda yang sedang bergerak mengalami gerak translasi dan rotasi. Suatu benda dikatakan setimbang apabila benda memiliki kesetimbangan translasi dan kesetimbangan rotasi. Dengan demikian, syarat kesetimbangan benda adalah resultan gaya dan momen gaya terhadap suatu titik sembarang sama dengan nol. Secara matematis kesetimbangan partikeldapat dituliskan :

ΣF_x = 0              ΣF_y = 0         dan        Στ = 0