Gerak rotasi (melingkar) adalah gerakan pada bidang datar yang lintasannya berupa lingkaran. kita akan mempelajari bagaimana suatu benda dapat berotasi dan apa yang menyebabkan. Oleh karena itu, kita akan mengawali dengan pembahasan tentang pengertian momen gaya, momen inersia, dan momentum sudut pada gerak rotasi.
Momen Gaya (Torsi) Pada Gerak Rotasi
Benda dapat melakukan gerak rotasi karena adanya momen gaya. Momen gaya timbul akibat gaya yang bekerja pada benda tidak tepat pada pusat massa.
Gambar diatas memperlihatkan sebuah gaya F bekerja pada sebuah benda yang berpusat massa di O. Garis/kerja gaya berjarak d, secara tegak lurus dari pusat massa, sehingga benda akan berotasi ke kanan searah jarum jam. Jarak tegak lurus antara garis kerja gaya dengan titik pusat massa disebut lengan gaya atau lengan momen. Momen gaya didefinisikan sebagai hasil kali antara gaya (F) dengan jarak lengan gaya (d). Secara matematis dapat ditulis sebagai berikut.
τ = F × d
Karena d = r × sin θ, maka persamaan di atas menjadi sebagai berikut.
τ = F × r × sin θ
Keterangan:
τ : momen gaya (Nm)
d : lengan gaya (m)
F :gaya (N)
r : jari-jari (m)
d : lengan gaya (m)
F :gaya (N)
r : jari-jari (m)
Arah momen gaya dinyatakan oleh aturan tangan kanan. Bukalah telapak tangan kanan kita dengan ibu jari terpisah dari keempat jari yang lain. Lengan gaya d sesuai dengan arah ibu jari, gaya F sesuai dengan arah keempat jari, dan arah torsi sesuai dengan arah membukanya telapak tangan.
Momen gaya τ menyebabkan benda berotasi. Jika benda berotasi searah jarum jam, maka torsi yang bekerja pada benda bertkita positif. Sebaliknya, jika benda berotasi dengan arah berlawanan dengan arah jarum jam, maka torsi penyebabnya bertkita negatif. Torsi-torsi yang sebidang dapat dijumlahkan.
Apabila pada sebuah benda bekerja beberapa gaya, maka jumlah momennya sama dengan momen gaya dari resultan semua gaya yang bekerja pada benda tersebut. Secara matematis dapat dituliskan seperti di bawah ini.
τO1 + τO2 + τO3 + …. Rd atau ΣτO = Rd
Momen Inersia Pada Gerak Rotasi
Momen inersia (kelembaman) suatu benda adalah ukuran kelembaman suatu benda untuk berputar terhadap porosnya. Nilai momen inersia suatu benda bergantung kepada bentuk benda dan letak sumbu putar benda tersebut.
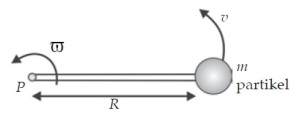
Misalkan kita memiliki sebuah batang ringan (massa diabaikan) dengan panjang R. Salah satu ujung batang, yaitu titik P, ditetapkan sebagai poros rotasi. Pada ujung batang yang lain dihubungkan dengan sebuah partikel bermassa m. Jika sistem diputar terhadap poros P , sehingga partikel berotasi dengan kecepatan v, maka energi kinetik rotasi partikel dapat ditulis sebagai berikut.
Karena v = R ω , maka
Momen inersia dilambangkan dengan I, satuannya dalam SI adalah kgm2. Nilai momen inersia sebuah partikel yang berotasi dapat ditentukan dari hasil kali massa partikel dengan kuadrat jarak partikel tersebut dari titik pusat rotasi. Faktor m × R2 merupakan momen inersia titik terhadap sumbu putarnya. Secara matematis dapat ditulis sebagai berikut.
I = m · R2
Keterangan:
I : momen inersia (kgm2)
R : jari-jari (m)
m : massa partikel atau titik (kg)
R : jari-jari (m)
m : massa partikel atau titik (kg)
Benda yang terdiri atas susunan partikel (titik), jika melakukan gerak rotasi memiliki momen inersia sama dengan hasil jumlah dari momen inersia partikel penyusunnya.
I = Σ mi x Ri2 = (m1 × R21) + (m2 × R22) + (m3 × R23) + …
Pada gambar berikut, dilukiskan momen inersia pada gerak rotasi berbagai benda tegar homogen.
Momentum Sudut Pada Gerak Rotasi
Pernahkah kita melihat orang bermain gasing? Mengapa gasing yang sedang berputar meskipun dalam keadaan miring tidak roboh? Pasti ada sesuatu yang menyebabkan gasing tidak roboh. Setiap benda yang berputar mempunyai kecepatan sudut. Bagaimana hubungan antara momen inersia dan kecepatan sudut?
Gambar di atas memperlihatkan titik A yang berotasi dengan sumbu putar O. R adalah jarak antara O dan A. Selama berotasi titik A memiliki momentum sebesar P = m × v. Hasil perkita momentum dengan jarak R disebut momentum sudut, dan diberi notasi L.
L = P × R
L = m × v × R
L = m × ω × R × R
L = m × R2 × ω
L = m × v × R
L = m × ω × R × R
L = m × R2 × ω
Apabila momentum sudut dihubungkan dengan momen inersia, maka diperoleh persamaan sebagai berikut.
L = I × ω
Keterangan:
v : kecepatan linear (m/s)
L : momentum sudut (kg m2s–1)
m : massa partikel/tittik (kg)
R : jarak partikel ke sumbu putar (m)
ω : kecapatan sudut (rad/s)
I : momen inersia (kg m2)
L : momentum sudut (kg m2s–1)
m : massa partikel/tittik (kg)
R : jarak partikel ke sumbu putar (m)
ω : kecapatan sudut (rad/s)
I : momen inersia (kg m2)
Momen Kopel Pada Gerak Rotasi
Kopel adalah pasangan dua gaya sama besar dan berlawanan arah yang garis-garis kerjanya sejajar tetapi tidak berimpit.
Besarnya kopel dinyatakan dengan momen kopel (M), yaitu hasil perkita salah satu gaya dengan jarak tegak lurus antara kedua gaya tersebut. Secra matematis dapat ditulis sebagai berikut.
M = F × d
Keterangan:
M : momen kopel (Nm)
F : gaya (N)
d : jarak antargaya (m)
F : gaya (N)
d : jarak antargaya (m)
Pengaruh kopel pada suatu benda memungkinkan benda tersebut berotasi. Jika kopel berotasi searah jarum jam diberi nilai negatif (–), dan jika berlawanan dengan arah jarum jam diberi nilai positif (+).
Contoh kopel adalah gaya gaya yang bekerja pada jarum kompas di dalam medan magnetik bumi. Pada kutub utara dan kutub selatan jarum, bekerja gaya yang sama besar, tetapi arahnya berlawanan.
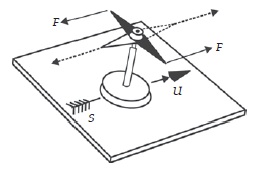 Gaya-gaya yang bekerja pada kedua kutub jarum kompas karena gerak rotasi
Gaya-gaya yang bekerja pada kedua kutub jarum kompas karena gerak rotasi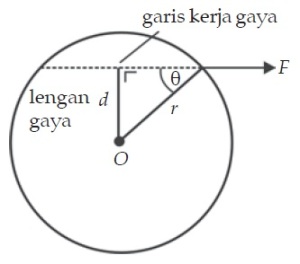







Tidak ada komentar:
Posting Komentar