Gerak Lurus Dengan Percepatan Konstan

Suatu partikel yang bergerak dengan percepatan konstan memiliki pertambahan kecepatan yang konstan, atau pertambahan kecepatan linear terhadap waktu. Apabila mulamula saat t = 0partikel bergerak dengan kecepatan ν₀, setelah t detik kecepatannya bertambah sebesar at. Kecepatannya setiap saat menjadi:

Partikel yang memiliki percepatan konstan kecepatan rata-rata partikel merupakan nilai tengah kecepatan awal dan kecepatan akhir. Hal ini ditunjukkan oleh gambar b dibawah. Apabila kecepatan mula-mula adalah ν₀ dan kecepatan akhirnya ν_t kecepatan rata-ratanya adalah :

Perpindahannya adalah :

Grafik posisi sebagai fungsi waktu ditunjukkan pada gambar c dibawah. Pada umumnya diambilt = 0 pada saat mula-mula, dengan x_o= 0 atau partikel mulai di x = 0. Kemudian jika t tersebut kita masukkan ke persamaan diatas maka kita peroleh :

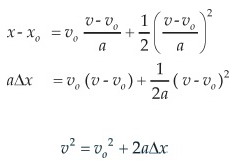
Gambar Grafik Gerak Lurus Dengan Percepatan Konstan

Dimana :

(a) Grafik percepatan sebagai fungsi waktu untuk percepatan konstan.
(b) Percepatan merupakan kemiringan grafik kecepatan sebagai fungsi waktu.
(c) Grafik fungsi posisi sebagai fungsi waktu.

Salah satu contoh gerak dengan percepatan konstan adalah gerak jatuh bebas. Sebuah benda atau partikel yang berada pada ketinggian tertentu mula-mula diam lalu dijatuhkan, benda bergerak ke bawah karena mendapat percepatan gravitasi sebesar g ke arah bawah.

Dari Persamaan diatas kita dapat memperoleh kecepatan benda setelah sampai di permukaan tanah adalah :

Kecepatan mula-mula adalah nol karena benda diam, bila posisi awal di atas permukaan tanah setinggi h dan posisi akhir di permukaan tanah, maka :

     sehingga      

Bagaimana bila sebuah partikel bergerak dengan percepatan tidak konstan tetapi merupakan fungsi waktu, sehingga kecepatannya juga fungsi waktu. Kita bisa mencari posisinya dengan menghitung luasan yang dibentuk oleh fungsi kecepatan dan sumbu t. Luasan di bawah fungsi sampai t tertentu adalalah posisi saat t tertentu tersebut berada. Luasan di bawah kurva bisa kita bagi menjadi N persegi panjang dengan lebar Δt dan tinggi (t), lebar Δt adalah = (t₂– t₁)/N, jika Δt sangat kecil maka jumlahan dapat dinyatakan sebagai :

Begitu juga mencari kecepatan dari suatu fungsi a(t). Jika kita mengetahui grafik fungsi a(t)sebagai fungsi waktu maka kecepatan adalah luasan di bawah fungsi a dengan fungsi t.