Senin, 02 Maret 2015

Proses Termodinamika

Proses termodinamika yang terjadi pada gas terdiri dari proses isobarik, proses isokorik, proses isotermis, dan proses adiabatik. Energi selalu berkaitan dengan usaha. Telah Anda ketahui bahwa usaha merupakan hasil perkalian gaya dengan perpindahan (W = F × s).

Proses Termodinamika

Proses termodinamika
Pada gambar diatas memperlihatkan penampang air silinder yang didalamnya terdapat gas piston (pengisap). Piston ini dapat bergerak bebas naik turun. Jika luas piston A dan tekanan gas P, maka gas akan mendorong piston dengan gaya F = P × A. Oleh karena itu, usaha yang dilakukan gas adalah W = F × Δs . Jika F = P × A, maka W = P × A × Δ s.
Dan jika  \Delta s=\frac{\Delta V}{A} , maka persamaannya menjadi seperti berkut.
W = P × Δ V               atau                W = P (V2 – V1)
Keterangan:
W : usaha (J)
P : tekanan tetap (N/m2)
V1 : volume awal (m3)
V2 : volume akhir (m3)

Jenis-Jenis Proses Termodinamika

Gas dalam ruang tertutup dapat mengalami beberapa proses yaitu proses isobarik, proses isokorik, proses isotermis, dan proses adiabatik.

Proses Isobarik

Proses yang berlangsung pada tekanan tetap dinamakan proses isobarik. Bila volume gas bertambah, berarti gas melakukan usaha atau usaha gas positif (proses ekspansi). Jika volume gas berkurang, berarti pada gas dilakukan usaha atau usaha gas negatif (proses kompresi). Usaha yang dilakukan oleh gas pada proses isobarik besarnya sebagai berikut.
W = p × Δ V atau W = p (V2 – V1)
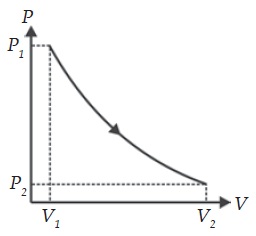
Usaha yang dilakukan gas terhadap lingkungannya atau kebalikannya sama dengan luas daerah bawah grafik tekanan terhadap volume (grafik p – V).
Proses Isobarik

Proses Isotermal

Proses isotermal adalah proses yang dialami gas pada suhu tetap. Usaha yang dilakukan gas pada proses ini tidak dapat dihitung dengan persamaan W = p × Δ V .
Proses Isotermal
Hal ini dikarenakan tekanannya tidak konstan. Namun, dapat diselesaikan dengan melakukan pengintegralan sebagai berikut.
W=\int_{v_{1}}^{v_{2}}pdV
Ingat p=\frac{nRT}{V}, maka W=\int_{v_{1}}^{v_{2}}\frac{nRT}{V}dV
karena n, R, dan T konstan, maka persamaannya menjadi sebagai berikut :
W=nRT\int_{v_{1}}^{v_{2}}\frac{dV}{V}
        =nRT[lnV]_{v_{1}}^{v_{2}}
        =nRT [lnV_{2}-lnV_{1}]
W=nRT\textit{ ln }\left ( \frac{V_{2}}{V_{1}} \right )

Proses Isokorik

Proses isokorik adalah proses yang dialami oleh gas di mana gas tidak mengalami perubahan volume atau volume tetap ( ΔV = 0 ). Oleh karena itu, usaha yang dilakukan gas pada proses isokorik adalah nol (W = p x 0 = 0 ).
Proses Isokorik

Proses Adiabatik

Pada proses isobarik, isotermal, dan isokorik dipengaruhi oleh lingkungan yaitu menerima atau melepaskan kalor. Proses adiabatik merupakan proses yang tidak ada kalor yang masuk atau keluar dari sistem (gas) ke lingkungan (Δ Q = 0) . Hal ini dapat terjadi apabila terdapat sekat yang tidak menghantarkan kalor atau prosesnya berlangsung cepat. Pada proses adiabatik berlaku rumus Poison.
Proses Adiabatik
pV^{\gamma }= \textup{Konstan}
p_{1}V_{1}^{\gamma }=p_{2}V_{2}^{\gamma }
Dengan γ merupakan perbandingan kalor jenis gas pada tekanan tetap (Cp) dan kalor jenis gas pada volum tetap (CV). Selanjutnya, perbandingan ini dinamakan tetapan Laplace.
\gamma =\frac{C_{p}}{C_{V}}
Untuk gas ideal, p=\frac{nRT}{V} , sehingga persamaan adiabatik di atas dapat ditulis dalam bentuk :
p_{1}V_{1}^{\gamma }=p_{2}V_{2}^{\gamma }
\frac{nRT_{1}}{V_{1}}V_{1}^{\gamma }=\frac{nRT_{2}}{V_{2}}V_{2}^{\gamma }
T_{1}V_{1}^{\gamma -1}=T_{2}V_{2}^{\gamma -1}
Adapun usaha pada proses adiabatik dapat dicari dengan cara sebagai berikut.
W=\int_{v_{1}}^{v_{2}}pdV
Karena p = CV-γ  , maka
W=\int_{v_{1}}^{V_{2}}CV^{-\gamma }dV=\frac{C}{1-\gamma }V^{1-\gamma }]_{v_{1}}^{v_{2}}=\frac{C}{1-\gamma }V^{1-\gamma }-V_{1}^{1-\gamma }
karena C = p1 V1γ = p2 V2γ , maka
W=\frac{1}{1-\gamma }(p_{2}V_{2}^{\gamma }V_{2}^{1-\gamma }-p_{1}V_{1}^{\gamma }V_{1}^{1-\gamma })
W=\frac{1}{1-\gamma }(p_{2}V_{2}-p_{2}V_{2})
Pada bagian sebelumnya Anda telah membahas mengenai energi dalam gas monoatamik. Anda juga mengetahui bahwa 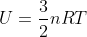U=\frac{3}{2}nRT, maka :
\Delta U=\frac{3}{2}nR\Delta T=\frac{3}{2}nR(T_{2}-T_{1})
Oleh karena itu, usaha yang dilakukan oleh sistem pada proses adiabatik dapat juga dituliskan :
W=-\Delta U=\frac{3}{2}nR(T_{2}-T_{1})
-

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)

Entri yang Diunggulkan

Barru WanuAku