Gerak parabola merupakan resultan dari gerak lurus beraturan pada sumbu X dan gerak lurus berubah beraturan pada sumbu Y. Gerak parabola merupakan salah satu contoh gerak pada bidang datar. Sebagai contoh gerak parabola adalah gerakan peluru yang ditembakan dari sebuah meriam dengan kecepatan awal tertentu dan dengan sudut kecondongan tertentu pula. Ternyata lintasan yang dilalui oleh peluru berupa lintasan melengkung yang disebut gerak parabola.
Gerak Parabola
Untuk memahami gerak parabola terlebih dahulu kita perhatikan hasil perpaduan gerak dari sebuah benda yang melakukan dua gerakan langsung pada bidang datar. Misalnya, persamaan gerak pada :
Sumbu x : Xt = 2t
Sumbu y : Yt = 4t – t2
Sumbu y : Yt = 4t – t2
(Xt dan Yt dalam cm; t dalam sekon)
Untuk mengetahui bentuk lintasan hasil perpaduannya terlebih dahulu kita lihat isi tabel di bawah ini!
Jika diambil nilai t yang berdekatan, maka grafik hasil perpaduan lintasan pada sumbu x dan sumbu y terlihat seperti di bawah ini.
 Persamaan gerak pada sumbu x adalah persamaan gerak lurus beraturan. Persaman gerak pada sumbu y adalah persamaan gerak lurus berubah beraturan diperlambat. Ternyata gerak hasil perpaduannya berupa gerak parabola.
Persamaan gerak pada sumbu x adalah persamaan gerak lurus beraturan. Persaman gerak pada sumbu y adalah persamaan gerak lurus berubah beraturan diperlambat. Ternyata gerak hasil perpaduannya berupa gerak parabola.
Untuk membahas gerak parabola, perhatikan dulu sketsa hasil pemotretan dua benda yang bergerak dari tempat yang sama.
Gambar diatas menunjukkan hasil pemotretan gerakan dua benda. Benda pertama jatuh bebas, sedangkan benda kedua dilempar dengan kecepatan awal v0 arah mendatar. Kedua benda jatuh ke bawah secara serempak. Gerakan arah vertikal mengikuti gerak lurus berubah beraturan dan gerak arah mendatar mengikuti gerak lurus beraturan. Lintasan yang dilalui oleh benda kedua adalah lintasan parabola.
Dalam tulisan berjudul Discorces On Two New Sciences, Galileo mengemukakan sebuah ide yang sangat berguna dalam menganalisis gerak parabola. Dia menyatakan bahwa gerak parabola dapat dipandang sebagai perpaduan gerak lurus beraturan pada sumbu horisontal (sumbu x) dan gerak lurus berubah beraturan pada sumbu vertikal (sumbu y) secara terpisah.
Persamaan Gerak Parabola
Tiap gerakan ini tidak saling mempengaruhi tetapi gabungannya tetap menghasilkan gerak menuju ke bumi. Bagaimanakah bentuk persamaan gerak parabola tersebut? Perhatikan gambar berikut!
 Gambar diatas merupakan sebuah benda yang dilempar dengan kecepatan awal vo dan sudut kecondongan (sudut elevasi) sebesar α sehingga benda melakukan gerak parabola.
Gambar diatas merupakan sebuah benda yang dilempar dengan kecepatan awal vo dan sudut kecondongan (sudut elevasi) sebesar α sehingga benda melakukan gerak parabola.
Jika kecepatan awal vo diuraikan pada sumbu x dan sumbu y di dapat vox dan voy dimana :
vox : vo cos α
voy : vo sin α
voy : vo sin α
Untuk selanjutnya mari kita bahas dulu gerakan benda pada sumbu x dan sumbu y
Gerak pada Sumbu x (Gerak Lurus Beraturan)
Kecepatan awal adalah vox = vo cos α
Karena gerak pada sumbu x adalah gerak lurus beraturan, maka kecepatan setelah t adalah :
vtx = vox = vo cos α
Perpindahan yang ditempuh setelah t adalah :
Xt = vox . t = vo cos α . t
Gerak pada Sumbu y (Gerak Lurus Berubah Beraturan)
Gerak pada sumbu y selalu mendapatkan percepatan αy = -g dimana g adalah percepatan gravitasi.
Kecepatan setelah t adalah Vty = Voy – gt
vty = vo sin α – gt
Perpindahan yang ditempuh setelah t adalah
Yt = vo sin α . t – 1⁄2gt2
Tempat Kedudukan Setiap Saat (TK)
Tempat kedudukan benda setiap saat dinyatakan dengan koordinat TK = (Xt, Yt)
Kecepatan dan Arah Kecepatan Setiap Saat
Kecepatan benda setiap saat merupakan resultan dari kecepatan benda pada arah sumbu x dan kecepatan benda pada arah sumbu y, sehingga kecepatan benda setiap saat :
vx = v0 cos α
vy = v0 sin α – gt
Jika arah kecepatan benda setiap saat dinyatakan dengan β, maka :
Kedudukan Benda di Tempat Tertinggi
Pada saat benda berada di tempat tertinggi (di titik A) arah kecepatan mendatar sehingga
vx = vo cos α dan vy = 0
atau
v = vx = vo cos α
vy = vo sin α – gt
O = vo sin α – gt
gt = vo sin α
vy = vo sin α – gt
O = vo sin α – gt
gt = vo sin α
Dengan demikian, waktu yang diperlukan untuk mencapai tempat tertinggi :
Pada saat benda mencapai tempat tertinggi, maka jarak mendatar yang ditempuh:
Tinggi maksimum yang dicapai :
Kedudukan Benda di Tempat Terjauh
Pada saat benda di tempat terjauh (di titik B) maka Yt = 0
Yt = V0 sin αt – ½ gt2
0 = V0 sin αt – ½ gt2
½ gt2 = V0 sin αt
t = (2V0 sin α)/g
Waktu yang diperlukan oleh sebuah benda untuk mencapai tempat terjauh :
Nilai tersebut dua kali dari nilai waktu yang diperlukan benda untuk mencapai tempat tertinggi. Jarak mendatar yang ditempuh pada saat mencapai tempat terjauh :
Percobaan Gerak Parabola
Letakkan posisi selang plastik kecil seperti gambar (a). Tutup ujung selang plastik B dengan jari tangan dan isikan air pada selang plastik melalui ujung A setinggi h. Lepaskan ujung jari penutup dan amati jatuhnya air pada lantai. Ukur jarak terjauh yang dicapai oleh air pertama kali.
Ulangi langkah di atas dengan mengubah sudut elevasi selang seperti gambar (b). Ukur jarak terjauh yang dicapai oleh air pertama kali!
 Bagaimanakah jarak mendatar yang dicapai oleh air pada langkah pertama? Bagaimanakah jarak mendatar yang dicapai oleh air pertama kali pada langkah kedua? Apakah yang dapat disimpulkan dari percobaan gerak parabola tersebut ?
Bagaimanakah jarak mendatar yang dicapai oleh air pada langkah pertama? Bagaimanakah jarak mendatar yang dicapai oleh air pertama kali pada langkah kedua? Apakah yang dapat disimpulkan dari percobaan gerak parabola tersebut ?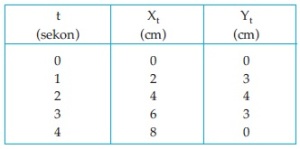





Tidak ada komentar:
Posting Komentar