Kamis, 26 Februari 2015

Pengolahan Data Pengukuran SMA Kelas X

Pengukuran dalam fisika bertujuan untuk mendapatkan data. Apakah manfaat data yang diperoleh adalah dapat dipelajari sifat-sifat alam dari besaran yang sedang diukur. Dari data itu pula dapat dilakukan prediksi kejadian berikutnya. Dari penjelasan tersebut dapat dilihat betapa pentingnya arti data hasil pengukuran. Namun perlu kita ketahui bahwa untuk memenuhi pemanfaatannya data yang ada perlu dianalisa atau diolah. Metode pengolahan data sangat tergantung pada tujuan pengukuran (eksperimen) yang dilakukan. Sebagai contoh untuk kelas X SMA ini dapat dikenalkan tiga metode analisa data seperti berikut.

Metode Generalisasi

di tingkat SMA ada yang bertujuan untuk memahami konsep-konsep yang ada. Misalnya mempelajari sifat-sifat massa jenis air. Untuk mengetahui sifat itu maka dapat dilakukan pengukuran kemudian datanya diolah. Pengolahan data untuk tujuan ini tidak perlu rumit, cukup dari data yang ada dibuat simpulan yang berlaku umum. Salah satu metode untuk membuat simpulan masalah seperti ini adalah metode generalisasi.

Metode Kesebandingan

Tujuan pengukuran (eksperimen) yang utama adalah mencari hubungan antara besaran yang satu dengan besaran yang lain. Dari hubungan antar besaran ini dapat diketahui pengaruh antar besaran dan kemudian dapat digunakan sebagai dasar dalam memprediksi kejadian berikutnya. Misalnya semakin besar massa balok besi maka semakin besar pula volume balok besi tersebut.
Untuk memenuhi tujuan pengukuran di atas maka data yang diperoleh dapat dianalisa dengan cara membandingkan atau disebut metode kesebandingan. Dalam metode kesebandingan ini sebaiknya data diolah dengan menggunakan grafik. Untuk tingkat SMA ini dapat dipelajari dua bentuk kesebandingan yaitu berbanding lurus dan berbanding terbalik.

Berbanding Lurus

Dua besaran yang berbanding lurus (sebanding) akan mengalami kenaikan atau penurunan dengan perbandingan yang sama. Misalnya X berbanding lurus dengan Y, maka hubungan ini dapat dituliskan seperti berikut.
X\sim Y
\frac{X_{1}}{Y_{1}}=\frac{X_{2}}{Y_{2}}
Hubungan berbanding lurus ini dapat digambarkan pada grafik dengan kurva yang linier seperti pada gambar berikut.
Grafik X berbanding lurus dengan Y
Grafik X berbanding lurus dengan Y,metode berbanding lurus,penulisan metode berbanding lurus

Berbanding Terbalik

Dua besaran akan memiliki hubungan berbanding terbalik jika besaran yang satu membesar maka besaran lain akan mengecil tetapi pernya tetap. Misalnya X berbanding terbalik dengan Y, maka hubungan ini dapat ditulis sebagai berikut :
X\sim \frac{1}{Y}\rightarrow X \cdot Y = C
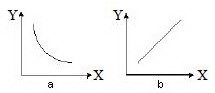
Grafik Y berbanding terbalik dengan X
Grafik Y berbanding terbalik dengan X,metode berbanding terbalik,grafik metode berbanding terbalik,penulisan metode berbanding terbalik
Hubungan berbanding terbalik ini dapat digambarkan pada grafik dengan kurva yang berbentuk hiperbola pada satu kuadran (untuk X dan Y positif) seperti pada gambar a diatas  atau linier seperti yang terlihat pada gambar b diatas.

Metode Perhitungan Statistik

Dalam belajar fisika banyak ditemukan persamaan-persamaan, bahkan ada siswa yang mengatakan, fisika itu rumus. Rumus-rumus fisika merupakan bentuk singkat dari suatu konsep, hukum atau teori fisika. Salah satu pemanfaatan rumus fisika adalah untuk perhitungan dan pengukuran suatu besaran.
Besaran-besaran fisika ada yang dapat diukur langsung dengan alat ukur tetapi ada pula yang tidak dapat diukur langsung. Besaran yang belum memiliki alat ukur inilah yang dapat diukur dengan besaran-besaran lain yang punya hubungan dalam suatu perumusan fisika. Contohnya mengukur massa jenis benda. Besaran ini dapat diukur dengan mengukur massa dan volume bendanya, kemudian massa jenisnya dihitung dengan rumus berikut.
\rho =\frac{m}{V}
Apakah pengukuran yang hanya dilakukan satu kali dapat memperoleh data yang akurat? Jawabnya tentu tidak. Kita sudah mengetahui bahwa pada pengukuran banyak terjadi kesalahan. Untuk memperkecil kesalahan dapat dilakukan pengukuran berulang. Nilai besaran yang diukur dapat ditentukan dari nilai rata-ratanya. Perhitungan ini dinamakan perhitungan statistik. Metode ini dapat dibantu dengan tabel seperti pada tabel statistik dibawah. Bahkan pada analisa ini dapat dihitung kesalahan mutlak (standar deviasi) dari pengukuran.
Tabel Statistik
Tabel Statistik,metode Statistik,penyelesaian metode Statistik
Dari tabel statistik diatas dapat dihitung nilai rata-rata x dan kesalahan mutlak dengan persamaan statistik seperti di bawah.
\bar{x}\frac{\sum x}{n}
\Delta x =\sqrt{\frac{\sum \left | x-\bar{x} \right |}{n(n-1)}}
dengan :
x = nilai rata-rata
Δx = nilai kesalahan mutlak pengukuran
-

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)

Entri yang Diunggulkan

Barru WanuAku