Minggu, 22 Februari 2015

Gerak Translasi

Gerak translasi adalah gerak suatu benda dimana setiap titik pada benda tersebut menempuh lintasan dan bentuk yang sama. Lintasan pada gerak translasi dapat berupa garis lurus atau bukan. Hal ini terjadi karena syarat sebuah gerak translasi adalah “setiap titik pada benda tersebut menempuh lintasan dan bentuk yang sama”. seperti ilustrasi gerka translasi berikut.
Gerak Translasi Dengan Lintasan LurusGerak Translasi Dengan Lintasan Lurus
Gerak Translasi Dengan Lintasan MelengkungGerak Translasi Dengan Lintasan Melengkung

Perpindahan Dan Jarak Pada Gerak Translasi

Kalian sering mendengar atau mengucapkan kata bergerak. Apa sebenarnya arti bergerak dalam ilmu fisika? Apakah kalian sudah mengerti? Benda dikatakan bergerak jika mengetahui perubahan posisi atau kedudukan. Coba kalian lihat gambar berikut.
Gerak Translasi
Posisi atau kedudukan titik A dan titik B dapat dituliskan sebagai vektor dua dirumuskan sebagai berikut.
r = xi + yj
Partikel dari titik A pindah ke titik B maka partikel tersebut dikatakan telah bergerak dan perpindahannya memenuhi persamaan berikut.
Δr = rB − rA     atau    Δr = Δxi + Δyj
Jarak tempuh
Perpindahan partikel pada gambar diatas digambarkan sebagai vektor dari A ke B yaitu vektor Δr. Bagaimana dengan jarak tempuhnya? Jarak tempuh partikel adalah panjang lintasan yang dilakukan partikel selama bergerak.

Kecepatan Dan Laju Gerak Translasi

Setiap benda yang bergerak selalu mengalami perpindahan. Perpindahan yang terjadi tiap satu satuan waktunya diukur dengan besaran yang dinamakan kecepatan. Di kelas X kalian telah belajar tentang kecepatan. Apakah masih ingat? Coba kalian perhatikan penjelasan berikut.

Kecepatan dan kelajuan rata-rata

Jika kita naik mobil atau sepeda motor, kecepatannya tidaklah tetap. Kadang bisa cepat dan kadang lambat, bahkan saat lampu merah harus berhenti. Pada gerak dari awal hingga akhir dapat diperoleh suatu kecepatan yang dinamakan kecepatan rata-rata dan didefinisikan sebagai perpindahan tiap satu satuan waktu. Perumusannya sebagai berikut.
\bar{v}=\frac{\Delta r}{\Delta t}
Laju rata-rata. Bagaimana dengan laju rata-rata? Kecepatan adalah besaran vektor maka berkaitan dengan perpindahan. Tetapi laju merupakan besaran skalar maka harus berkaitan dengan jarak tempuh. Sehingga laju ratarata didefinisikan sebagai jarak tempuh yang terjadi tiap satu satuan waktu.
\bar{v}=\frac{S}{t}

Kecepatan dan kelajuan sesaat

Kalian tentu masih ingat di kelas X tentang kecepatan sesaat. Kecepatan sesaat merupakan kecepatan yang terjadi pada saat itu saja. Contohnya pada saat lampu merah kecepatan mobil sebesar nol, kemudian saat lampu hijau mobil tersebut diberikan kecepatan 20 km/jam ke utara.
Secara matematik kecepatan sesaat ini dapat dirumuskan sebagai deferensial atau turunan fungsi yaitu fungsi posisi. Jadi kecepatan sesaat adalah deferensial dari posisinya.
\bar{v}=\frac{dr}{dt}
Sedangkan laju sesaat dapat ditentukan sama dengan besar kecepatan sesaat. Laju sesaat inilah yang dapat diukur dengan alat yang dinamakan speedometer.
Sudah tahukah kalian dengan deferensial fungsi itu? Tentu saja sudah. Besaran posisi atau kecepatan biasanya memenuhi fungsi waktu. Deferensial fungsi waktu tersebut dapat memenuhi persamaan berikut.
Jika r = tn maka 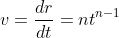v=\frac{dr}{dt}=nt^{n-1}
Pada gerak dua dimensi, dapat dijelaskan dengan contoh gerak perahu seperti pada gambar berikut.
Kecepatan dan kelajuan sesaat gerak translasi
Secara vektor, kecepatan perahu dapat diuraikan dalam dua arah menjadi vx dan vy. Posisi tiap saat memenuhi P(x,y). Berarti posisi perahu atau benda dapat memenuhi persamaan diatas. dari persamaan itu dapat diturunkan persamaan kecepatan arah sumbu x dan sumbu y sebagai berikut.
r = xi + yj
\frac{dr}{dt}=\frac{xd}{dt}i+\frac{dy}{dt}j
v = vxi + vy j
Jadi proyeksi kecepatannya memenuhi :
v_{x}=\frac{dx}{dt}\textup{ dan }v_{y}=\frac{dy}{dt}
Besar kecepatan sesaat, secara vektor dapat memenuhi dalil Pythagoras. Kalian tentu dapat merumuskan persamaan besar kecepatan tersebut. Perhatikan persamaan diatas Dari persamaan itu dapat kalian peroleh :
\left | v \right |=\sqrt{v_{x}^{2}+v_{y}^{2}}

Posisi dan kecepatan

Jika kecepatan sesaat dapat ditentukan dengan deferensial posisi maka secara matematis posisi dapat ditentukan dari integral kecepatan sesaatnya. Integral ini dapat dirumuskan sebagai berikut.
r=r_{0}+\int vdt
Seperti yang telah kalian pelajari bahwa kecepatan merupakan deferensial dari fungsi posisi. Dengan grafik, kecepatan sesaat dapat menyatakan gradien garis singgung fungsi posisi.
Posisi Gerak Translasi
Kecepatan pada saat t dapat dirumuskan :
v = tg ∞
Sedangkan posisi suatu benda pada t s merupakan integral dari fungsi kecepatannya. Bagaimana jika diketahui dalam bentuk grafik seperti pada gambar berikut.
Kecepatan Gerak Translasi
Tentu kalian dapat menjawabnya bahwa posisi suatu benda dapat dibentuk dari luas grafik (terarsir), sehingga diperoleh persamaan :
r = ro + luas daerah terarsir

Percepatan Gerak Translasi

Nilai rata-rata dan sesaat

Sesuai dengan kecepatan, percepatan juga memiliki dua nilai. Percepatan rata-rata didefinisikan sebagai perubahan kecepatan tiap satu satuan waktu.
\bar{a}=\frac{\Delta v}{\Delta t}
Sedangkan percepatan sesaat dapat ditentukan dengan deferensial dari kecepatan sesaatnya.
\bar{a}=\frac{dv}{dt}

Kecepatan dan percepatan

Jika percepatan sesaat dapat ditentukan dengan deferensial dari kecepatan sesaat maka sebaliknya berlaku integral berikut.
v=v_{0}+\int adt
-

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)

Entri yang Diunggulkan

Barru WanuAku